POLINOMIOS: SUMA, RESTA, MULTIPLICACIÓN Y DIVISIÓN
POLINOMIOS
Un polinomio es una expresión
algebraica de la forma:
P(x)
= an xn + an − 1 xn −
1 + an − 2 xn − 2+ ... + a1x1 + a0
Siendo:
an, an−1 ...
a1, ao números, llamados coeficientes
n un número natural
x la variable o indeterminada
an es el coeficiente
principal
ao es el término
independiente
DEFINICION: Polinomio, en matemáticas, se
denomina a la suma de varios monomios,
llamados términos del polinomio. Es una expresión algebraica constituida
por una o más variables, utilizando solamente operaciones de adición, sustracción, multiplicación y exponentes numéricos
positivos. El polinomio de un sólo término se denomina monomio, el
de dos binomio, el de tres trinomio.
GRADO
DE UN POLINOMIO
El
grado de un polinomio P(x) es el mayor exponente al que se encuentra elevada la
variable x.
Según
su grado los polinomios pueden ser de:
TIPO
|
EJEMPLO
|
PRIMER
GRADO
|
P(x)
= 3x + 2
|
SEGUNDO
GRADO
|
P(x)
= 2x2 + 3x + 2
|
TERCER
GRADO
|
P(x)
= x3 − 2x2 + 3x + 2
|
Tipos
de polinomios
Polinomio
nulo
Es
aquel polinomio que tiene todos sus coeficientes nulos.
P(x)
= 0x2 + 0x + 0
Polinomio
homogéneo
Es
aquel polinomio en el que todos sus términos o monomios son del mismo grado.
P(x)
= 2x2 + 3xy
Polinomio
heterogéneo
Es
aquel polinomio en el que no todos sus términos no son del mismo grado.
P(x)
= 2x3 + 3x2 − 3
Polinomio
completo
Es
aquel polinomio que tiene todos los términos desde el término independiente
hasta el término de mayor grado.
P(x)
= 2x3 + 3x2 + 5x − 3
Polinomio
incompleto
Es
aquel polinomio que no tiene todos los términos desde el término independiente
hasta el término de mayor grado.
P(x)
= 2x3 + 5x − 3
Polinomio
ordenado
Un
polinomio está ordenado si los monomios que lo forman están escritos de mayor a
menor grado.
P(x)
= 2x3 + 5x − 3
Polinomios
iguales
Dos
polinomios son iguales si verifican:
Los
dos polinomios tienen el mismo grado.
Los
coeficientes de los términos del mismo grado son iguales.
P(x)
= 2x3 + 5x – 3
Q(x)
= 5x − 3 + 2x3
Polinomios
semejantes
Dos polinomios
son semejantes si verifican que tienen la misma parte literal.
P(x)
= 2x3 + 5x − 3
Q(x)
= 3x3 + 7x − 2
SUMA DE POLINOMIOS.
La suma de polinomios es
una operación en la que partiendo de dos polinomios P(x) y
Q(x), obtenemos un tercero R(x), que es la suma de los dos
anteriores, R(x) tiene por coeficiente de cada monomio el de la suma de
los coeficientes de los monomios de P(x) y Q(x) del mismo grado. Dados los
dos polinomios P(x) y Q(x).
La
suma se puede hacer de dos formas distintas: en horizontal y en vertical. Vamos
a ver las dos maneras, y después puedes elegir cuál te resulta más fácil
para utilizar.
Suma
de polinomios en horizontal
Para
hacer las operaciones en horizontal primero escribimos un polinomio y seguido
en la misma línea escribimos el otro que vamos a sumar o restar. Después, agrupamos
términos semejantes.
Ejemplo:
Vamos a realizar la suma. Para ello escribimos cada
uno rodeado de paréntesis y con el signo de la suma entre ellos.
Fíjate
en los términos que son semejantes entre los dos polinomios. No podemos sumar
dos términos que tienen distinto grado, solo podemos agrupar los que sean
semejantes y después sumar.
Suma de polinomios en vertical
Para hacer las sumas en vertical
debemos escribir el primer polinomio ordenado. En el caso de que sea incompleto
es conveniente dejar los huecos libres de los términos que falten. Después,
escribimos el siguiente polinomio debajo del anterior, de manera que coincida
justo debajo el término semejante al de arriba. Después, ya podemos sumar
cada columna.
Fíjate en el primer polinomio. Hay que
escribirlo ordenado y ver si está completo. En este caso falta el término de
grado 3, entonces debemos dejar el hueco correspondiente o escribir un cero en
su lugar.
Ahora escribimos el segundo debajo del primero, de manera que coincidan los términos semejantes uno debajo de otro.
SUMA HORIZONTAL
Solo queda sumar cada columna, es decir, sumar los términos semejantes.
Ya has aprendido a sumar polinomios de
dos maneras diferentes: en horizontal y en vertical. ¿Cuál te ha parecido más
sencilla?
RESTA
DE POLINOMIOS
En esta operación dada la suma de dos
sumandos (llamada minuendo)
y uno de los sumandos (llamado sustraendo),
se busca el otro sumando (llamado resta
o diferencia).
Es decir, que la suma del sustraendo y la resta o diferencia, es igual al minuendo.
Es decir, que la suma del sustraendo y la resta o diferencia, es igual al minuendo.
Si de “a” (minuendo) queremos restar “b” (sustraendo), la diferencia será “a – b”
Y ésta será la diferencia si sumada con el sustraendo “”b” es igual al minuendo “a”
Regla
general para restar
Se escribe el minuendo con sus propios signos y
a continuación el sustraendo con
los signos cambiados y se reducen los términos semejantes, si los
hay.
Recuerda que si un término no tiene escrito su signo, el término es positivo
Veamos ejemplos:
Recuerda que si un término no tiene escrito su signo, el término es positivo
Veamos ejemplos:
Multiplicación de monomios con
polinomios:
Se le llama multiplicación de monomios
con polinomios cuando un solo factor se encuentra multiplicando a un polinomio.
Reglas:
- Se
multiplica el término del monomio por cada término del polinomio, sumando
los exponentes de las literales iguales.
- Se
coloca el signo de acuerdo con las reglas de los signos vistas
anteriormente
- Se
encuentra la suma algebraica de los productos parciales.
Multiplicación
de polinomios.
La multiplicación de polinomios es la
más general de las multiplicaciones algebraicas en este caso se multiplican un
polinomio con otro polinomio su resultado puede ser un polinomio, un número o
cero.
Reglas:
- Se
multiplica cada término del polinomio por cada término del polinomio,
sumando los exponentes de las literales iguales.
- Se
coloca el signo de cada factor resultante de acuerdo con las reglas de los
signos vistas anteriormente
- Se
encuentra la suma algebraica de los productos parciales.
Ejemplos:
FORMA HORIZONTAL
Presentación
de ejemplo dinámico
http://www.aulafacil.com/algebra/curso/e12.html
DIVISION
DE POLINOMIOS
Es la operación que tiene por objeto,
dado el producto de dos factores dividendo y
uno de los factores divisor encontrar
otro factor llamado cociente:
D = d · C
Donde:
D es el Dividendo (producto
de los factores “d” y “C”)
d es el divisor (factor conocido)
d es el divisor (factor conocido)
C es el cociente (factor desconocido)
Los factores “D”, “d” y “C” pueden ser
números, monomios o polinomios.
Leyes que sigue la división:
Ley de signos: el resultado es
negativo si la cantidad de factores negativos es impar, de lo contrario es
positivo.
(+) ÷ (+) = +
(-) ÷ (-) = +
(+) ÷ (-) = -
(-) ÷ (+)=-
(-) ÷ (-) = +
(+) ÷ (-) = -
(-) ÷ (+)=-
Ley de los
cocientes de los coeficientes: el
coeficiente del cociente es el cociente de dividir el coeficiente del dividendo
entre el coeficiente del divisor.
mx ÷ nxy = (m ÷ n)(x ÷ xy)
Donde m y n son números y n es
distinto de cero.
Ley de
exponentes: la
división de dos o más potencias de la misma base es igual a la
base elevada a la diferencia de las potencias.
Nota: resulta útil y cómodo colocar la
división como una expresión fraccionaria así:
División entre fracciones
En este tipo de división se cumplen
las mismas reglas que con la división de monomios y las reglas de división de
fracciones de la aritmética.
- Se
aplica ley de signos
- Se
multiplica el dividendo del primer término por el divisor del segundo para
crear el dividendo de la división, y el divisor del primero por el
dividendo del segundo para crear el divisor de la división (esto se llama
división cruzada)
- Se
divide el coeficiente del dividendo entre el coeficiente del divisor
- Se
aplica ley de los exponentes tomando las letras que no se encuentren como
elevadas a cero (nº = 1), y se escriben en orden alfabético.
Ejemplos:
División
entre polinomios.
En este tipo de división se procede de
manera similar a la división aritmética los pasos a seguir son los siguientes.
- Se
ordenan los polinomios con respecto a una misma letra y en el mismo
sentido (en orden ascendente u orden descendente), si el polinomio no es
completo se dejan los espacios de los términos que faltan.
- El
primer termino del cociente se obtiene dividiendo el primer termino del
dividendo entre el primer miembro del divisor.
- Se
multiplica el primer término del cociente por todos los términos del
divisor, se coloca este producto debajo de él dividendo y se resta del
dividendo.
- El
segundo término del cociente se obtiene dividiendo el primer termino del
dividendo parcial o resto (resultado del paso anterior), entre el primer
termino del divisor.
- Se
multiplica el segundo término del cociente por todos los términos del
divisor, se coloca este producto debajo de él dividendo parcial y se resta
del dividendo parcial.
- Se
continua de esta manera hasta que el resto sea cero o un dividendo parcial
cuyo primer término no pueda ser dividido por el primer termino del
divisor.
Cuando esto ocurre el resto será el
residuo de la división.
La intención con este método de
división es que con cada resta se debe eliminar el termino que se encuentra más
a la izquierda en el dividendo o dividendo parcial.
Presentación
de ejemplo dinámico.
División Sintética
La división sintética se realiza para
simplificar la división de un polinomio entre otro polinomio de la forma x – c,
logrando una manera mas compacta y sencilla de realizar la división.
Ilustraremos como el proceso de
creación de la división sintética con un ejemplo:
Comenzamos dividiéndolo normalmente
Pero resulta mucho escribir pues
repetimos muchos términos durante el procedimiento, los términos restados
pueden
quitarse sin crear ninguna confusión, al igual que no es necesario bajar los
términos
. al eliminar
estos términos repetidos el ejercicio nos queda:
Ahora si mantenemos las potencias
iguales de x en las columnas de cada potencia y colocando 0 en las faltantes se
puede eliminar el escribir las potencias de x, así:
Como para este tipo de división solo
se realiza con para divisores de la forma x – c entonces los coeficientes de la
parte derecha siempre son 1 – c, por lo que podemos descartar el coeficiente 1
y el signo negativo, también se puede lograr una forma más compacta al mover
los números hacia arriba, nos queda de la siguiente forma:
Si ahora insertamos a la primera
posición del último renglón al primer coeficiente del residuo (2), tenemos que
los primeros números de este renglón son los mismos coeficientes del cociente y
el último número es el residuo, como evitamos escribir dos veces eliminamos el
cociente.
Esta última forma se llama división
sintética, pero ¿como hacerla sin tanto paso?, ahora les presentamos los pasos
para llevar a cavo la división sintética:
- Se
ordenan los coeficientes de los términos en un orden decreciente de
potencias de x hasta llegar al exponente cero rellenando con coeficientes
cero donde haga falta
- Después
escribimos “c” en la parte derecha del renglón
- Se
baja el coeficiente de la izquierda al tercer renglón.
- Multiplicamos
este coeficiente por “c” para obtener el primer número del segundo renglón
(en el primer espacio de la izquierda nunca se escribe nada).
- Simplificamos
de manera vertical para obtener el segundo número del tercer renglón.
- Con
este último número repetimos los pasos cuatro y cinco hasta encontrar el
último número del tercer renglón, que será el residuo.
Para generalizar hace falta notar que
el signo que tenga el divisor no debe ser necesariamente
negativo. Para el uso de este método puede ser positivo o negativo.





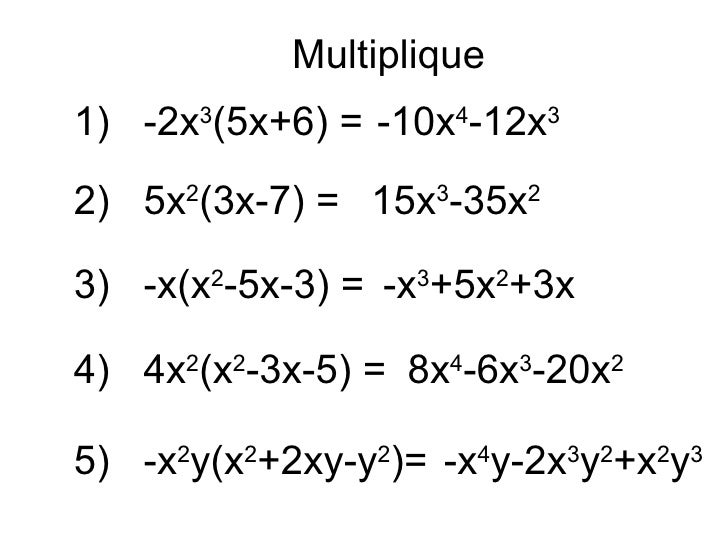

Alguien me podría decir el procedimiento de está multiplicacion de polinomios
ResponderEliminaresta vastante largo todo gracias
EliminarTENES QUE NASHEEEEEEEEE
ResponderEliminarNashe
Eliminarnasheeeeee
EliminarHola profesoras, el resultado del 4to ejercicio de multiplicación de polinomios está mal. El resultado correcto es: 4x^4-12x^3-20x^2. Abrazo y muy buen blog
ResponderEliminar